If you're new to coding and have struggled to learn recursion with fibonacci or exponential functions, then this article is for you. I had trouble with the concepts at first because I couldn't quite wrap my head around the "bubbling up" return values. Luckily, if we remove the return values from the equation, things become much more straightforward. So today let's focus on the true fundamentals of recursion by iterating through an array.
What is recursion?
For a function to be recursive, it only has to do 2 things:
- Call itself
- Know when to stop calling itself
That's it, that's all it takes. Technically, you don't even need the second one. Sure, without it your function will explode, but it'll explode recursively.
Let's build a simple function
To start off, let's make a base function. All it does is log a value in an array:
- a - b - c
You might notice that the way to log each value is to call it with the index that's one bigger. Right now we are the ones calling the function and incrementing the index...what if the function itself did the incrementing?
Making the function recursive
Let's add the incrementing and calling inside the function.
There it is: a recursive function. It looks odd to see a function call itself, however all programming languages are more than capable of doing this. However, if we ran this as is, it would blow up. That's because we never tell it to stop at any point. We still need requirement #2, a stop condition:
- a - b - c
Now, once we hit an index that's not in the array, it won't do anything and the whole chain of recursive functions comes to an end.
Guard clause
We could add a guard clause to remove the layer of nesting, but I think for illustrative purposes not using the inverse makes a little more intuitive sense. It's a fun challenge for you to try yourself!
What's actually happening
The secret sauce here is that our original "add one each time" logic is now being done inside the function with idx + 1. What really helps is seeing this graphically

As you can see, we keep increasing the value of our index by one each time, so we move through the entire array. While the index value changes, the array does not. Once there is no value at the index, the function has nothing more to do, and it completes. And since each function finished by calling another, the completion moves back up the chain, and we can move on with our program.
Take a minute to internalize what's happening here, because this is the heart of recursion
We can go deeper
Our function meets our definition of recursion, but it can't iterate through nested arrays recursively. This is no good, since that's actually one of the real-world applications for recursion. The reason for that is simple: if it ever runs into a nested object, it can just call itself again, this time from the start.
Can loops handle unknown depths?
Yes! Pretty much anything that can be done with recursion can also be done with iteration. The problem is elegance. While you can loop to unknown depths, you'll need some other helper structure like a stack or queue.
To account for nesting, all we need to do is add a step where we check if the value is an array. If it is, we start over at index 0, if not, we carry on as we normally would:
- a - x - y - b
Let's visualize what's going on here:
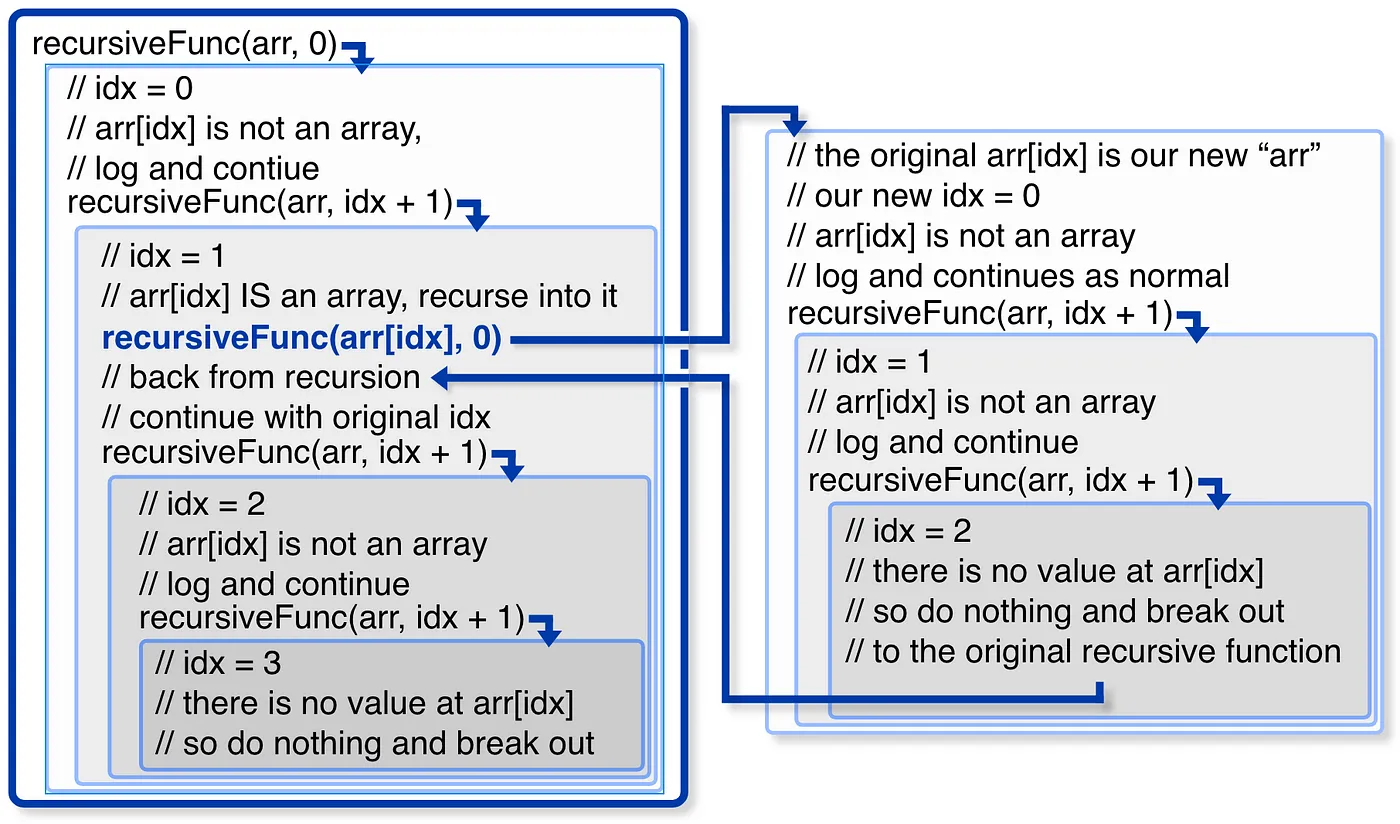
That new line is checking to see if the value is an array. If it is, look at how we pass in the new array and start a new index at 0 to restart the new sequence. Then, once that sequence is done, we come back to our main chain. Also, notice that the final recursiveFunc call is after and outside of the array check. That's because after we go down into an array, we always want to keep going when we come back up.
For simplicity, we passed in an array with only a single level of nesting. Once you understand what's going on here, try passing in another level of nesting and see if you can predict what will happen.
Double check by getting fancy
To make absolutely sure you understand the main concept, why not try adding another parameter? Let's add a level parameter for nicer printing:
a b - q - - x - r c
Notice where we +1 the idx vs level, it's not the same! We only increase level if we are dealing with a nested array, and we only increase idx if we are moving forward in an array, and not when we restart a new nested array. Now that the basics are done, it should be much easier to learn about recursive return values. Check out how they work with the fibonacci interview question.
Drawbacks to recursion
If recursion is so simple, why don't we use it everywhere? Why are loops better for pure iterations? One of the reasons has to do with the JavaScript Call Stack. I recommend checking it out, it's a fundamental part of programming. The long and short of it is: when you call a function, it gets placed on the call stack. Once it's finished, it's removed. However, the problem with recursion is that the first call can't finish until all of the children functions finish. That means the call stack gets taller and taller. If it gets too high, it will all break.
That's the issue with recursion, there is a maximum depth. You want one function that has a for loop that a million iterations? Well that's all fine and dandy. But a recursive function can start hitting issues way quicker. That doesn't mean loops are better. It just means we have to use recursion for more specific problems, like unknown depth or recursive data structures like Binary Search Trees. It's about finding the right tool for the problem.
If we're being honest though, the biggest reason developers don't use recursion is because it's harder to understand. Perhaps now you'll use it more after reading this article, eh?
Happy coding everyone,
Mike
Join the conversation on Reddit to leave a comment!